Tanto el libro como la aplicación infográfica Homograf.1 que lo acompaña, están por tanto dirigidos principalmente a arquitectos, arquitectos técnicos, aparejadores, delineantes y estudiantes de arquitectura, aunque puede ser útil también a ingenieros, arqueólogos y decoradores, que aplicando unos sencillos conceptos geométricos y dibujando en 2D con el programa AutoCAD 14, podrán conseguir un considerable ahorro de tiempo en las labores citadas, usando una herramienta sencilla, accesible y fácil de recordar, sin necesidad de recurrir ni a medios ni a personal especializado.

Una herramienta mecánica, anterior al ordenador, que constituye un valioso medio auxiliar en cualquier profesión técnica, y especialmente en la arquitectura, es la fotografía, que puede tener varias utilidades: como medio para disponer de un archivo gráfico, como complemento visual a una toma de datos relativa a un determinado edificio, generalmente para realizar un levantamiento de planos y también como procedimiento gráfico en sí, para los trabajos de elaboración y presentación de proyectos.

Recordemos que tanto la máquina fotográfica, como el laboratorio de revelado, han sido durante muchos años, en los que la reprografía no estaba al nivel actual ni al alcance de todos, un valioso auxiliar de la presentación de los proyectos arquitectónicos, especialmente en los casos en que se estima conveniente para una mejor expresión de un determinado proyecto, la presentación de determinadas fotografías de una maqueta de éste, la realización de un montaje gráfico de una perspectiva sobre la fotografía de un determinado entorno, o bien el llamado "fotomontaje" que consiste en la superposición de una fotografía de la maqueta, a una foto del entorno.

La gran utilidad de la fotografía como medio auxiliar para el trabajo del arquitecto, hace que éste se vea obligado a tener una cierta idea elemental de fotografía, pese a no haber estudiado oficialmente casi nada relacionado con esta materia. A nuestro entender, el momento idóneo para que los alumnos de arquitectura aprendan los principios básicos de la fotografía, puede ser cuando se empieza a estudiar la perspectiva cónica. Parece lógico aprender de forma simultánea fotografía y perspectiva cónica, ya que los principios geométricos de ambas son los mismos.

Por otra parte, es curioso también que la mayor parte de los citados estudiantes, no conozca, pese al interés que el tema despierta en todos los que se ven con necesidad de realizar alguna vez un levantamiento gráfico de un edificio, la denominada, en muchos de los programas de la asignatura Geometría Descriptiva, restitución perspectiva, aplicada a la extracción de medidas de cualquier fotografía. Esta carencia se debe, a que es un tema que actualmente se suele abordar en muy pocas Escuelas, dada su supuesta complejidad y sobre todo por la incomprensible tendencia general a reducir el tiempo dedicado a las materias gráficas básicas, en las carreras técnicas de la Universidad española.

La restitución perspectiva tiene por objeto la reconstrucción de una figura por medio de construcciones gráficas a partir de una perspectiva de ésta. Al considerar la fotografía como una perspectiva cónica, se denomina restitución fotográfica, rectificación fotográfica o también por algún autor, fotogrametría elemental, a esta reconstrucción a partir de un solo fotograma.

Por otra parte, conocemos como fotogrametría estereoscópica o simplemente fotogrametría, la técnica de restitución cuando ésta se realiza a partir de dos fotografías de orientación conocida, lo que constituye un problema que requiere profesionales especialistas en la materia. Esta técnica, que resulta imprescindible para el levantamiento de determinadas formas arquitectónicas, puede no ser necesaria, como veremos aquí, en los frecuentes casos de paramentos planos, donde podemos obtener con facilidad y precisión los datos métricos a partir de una sola fotografía y de determinadas medidas reales.

En la búsqueda de un procedimiento sencillo y accesible tanto para profesionales como para estudiantes, en esta publicación se recogen diversos métodos para la resolución de los citados problemas gráficos. En primer lugar se apuntan los procedimientos con herramientas manuales, que han constituido la base práctica de la que ha partido la idea de la aplicación infográfica, ya que la resolución gráfica manual de una figura afín u homóloga de otra dada, es una labor absolutamente "mecánica" que depende del dibujante y que quizá resulte, según los casos, larga y poco precisa.

Este análisis y otras razones nos hicieron llegar a la conclusión de que tener una aplicación como Homograf.1, sencilla de aprender y muy fácil de aplicar, que resuelve directamente las homografías planas, supone un adelanto de trabajo y sobre todo un aumento de precisión muy considerable en las citadas labores gráficas de los estudios de arquitectura.

Dado que AutoCAD es el programa de dibujo por ordenador utilizado por la mayor parte de los estudios de arquitectura en España, se eligió éste como base para desarrollar esta aplicación. Lógicamente, este programa no contiene un comando directo que pueda resolver las transformaciones homográficas planas conocidas como homología y afinidad.

Se ha estructurado el libro en tres capítulos, de los que el primero es una introducción al concepto de homografía y cada uno de los dos siguientes está dedicado a una de las dos aplicaciones principales de la homografía en el dibujo arquitectónico, dejando el anexo final para las cuestiones técnicas de instalación y funcionamiento de Homograf.1, aplicación infográfica grabada en disquete que forma parte de la publicación.

La homografía es un término matemático, dentro del campo de la Geometría Proyectiva, que significa relación o correspondencia entre dos figuras geométricas. Aunque la homografía no es muy conocida de forma general por este nombre, ha sido y sigue siendo muy utilizada de forma manual por los dibujantes, en diversas e importantes cuestiones relativas a la representación gráfica, como por ejemplo, un cambio de escala o el trazado de una circunferencia en perspectiva axonométrica o cónica.

Pues bien, la aplicación infográfica Homograf.1 para el programa AutoCAD 14, permite resolver precisamente este problema en cualquiera de los casos, de forma automática, a partir del establecimiento de cuatro pares de puntos correspondientes en una y otra figura.

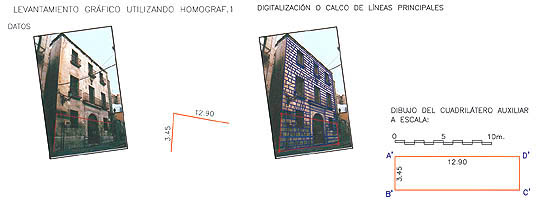
APLICACIÓN A LEVANTAMIENTOS DE FACHADAS
Cualquier fotografía de un paramento arquitectónico plano contiene en potencia, una importante información métrica que puede ser extraída. Estas medidas son imprescindibles para el correcto levantamiento gráfico, sobre todo en los frecuentes casos en que resulta imposible acceder a determinados puntos con una cinta métrica, y que en la práctica suelen ser todos los que se encuentran por encima de la planta baja del edificio en cuestión.

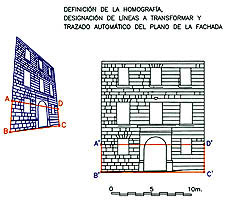
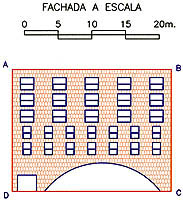
El procedimiento que se expone, se puede aplicar a cualquier toma fotográfica del tipo que sea. Los datos necesarios son la toma fotográfica y dos medidas, con lo que pasaremos a realizar la labor de despacho que conlleva las operaciones de digitalización de las líneas principales, dibujo del cuadrilátero auxiliar cuyas medidas son las dos (horizontal y vertical) de la toma de datos, determinación de la homografía utilizando Homograf, marcando los cuatro puntos de referencia en la digitalización de la fotografía y sus cuatro homólogos en la figura auxiliar dibujada, para que finalmente el ordenador realice de forma automática el cálculo y dibujo de la imagen homográfica que constituye el alzado a escala de la fachada.

APLICACIÓN AL TRAZADO DE PERSPECTIVAS LINEALES
Si por razones de economía de tiempo o de medios, únicamente necesitamos, partiendo de las plantas y alzados del proyecto, una perspectiva simplificada de un volumen arquitectónico que se pueda descomponer en caras planas, se puede realizar la perspectiva de dicho volumen en 2D con AutoCAD 14, con sencillez, rapidez y precisión, aplicando Homograf.1.

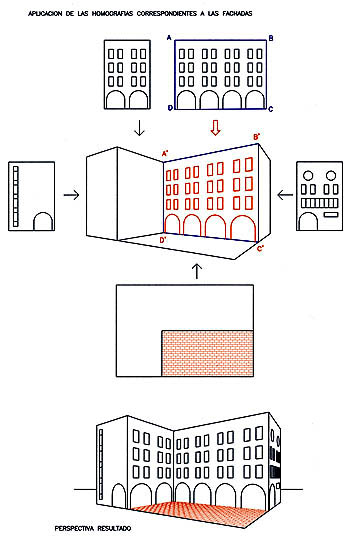
Cualquier perspectiva cónica o cilíndrica de un determinado volumen, que podemos considerar formado por un determinado número de caras o figuras planas, es sencillamente una proyección (cónica o cilíndrica) de todas éstas sobre un plano.

Homograf.1 permite, una vez dibujado el prisma contenedor del edificio en perspectiva axonométrica, completar la perspectiva de los "planos" de fachada mediante una homografía directa, marcando cuatro puntos cualesquiera de la figura de partida y sus cuatro homólogos en la perspectiva.

Del mismo modo también podremos realizar de forma simplificada una perspectiva de una fachada plana que ajuste sobre una fotografía cualquiera de un entorno determinado, sin tener que recurrir al clásico montaje gráfico-fotográfico de una perspectiva sobre una fotografía, que conlleva el dibujo de la perspectiva desde el mismo punto de vista desde el que se realizó la fotografía y que requiere normalmente medios especializados si se quiere realizar con precisión.

Del mismo modo Homograf puede tener su aplicación en el caso de tener que "reformar" una perspectiva ya realizada, con otras proporciones que nos interesen más normalmente por razones de percepción visual. Si a cualquier perspectiva cónica dibujada en 2D, le aplicamos una homografía, que transforme la retícula cuadrangular de éstas en una trapecial.

En definitiva Homograf.1 sirve para obtener una proyección de una figura plana a partir de otra proyección dada, pudiendo ser cualquiera de dichas proyecciones, cilíndrica ortogonal, cilíndrica oblicua o cónica, relacionando fácilmente por tanto todos los tipos de vistas y de perspectivas.

Enseguida nos daremos cuenta de que manejar Homograf es de una gran sencillez. Pero no debemos engañarnos, para que esta aplicación nos sea realmente útil, quizá sea conveniente que sepamos algo más. Pensemos que para dibujar arquitectura correctamente con una máquina, primero es necesario haber aprendido los principios básicos del dibujo técnico, para lo que, además de tener capacidad para imaginar proyecciones en el espacio, es imprescindible saber geometría; quizá debamos decir también que el aprendizaje de esta ciencia necesita de la experimentación y como ya le respondió Euclides al rey Tolomeo I de Egipto, en el año 300 a.C., para aprender geometría no hay caminos especiales, ni siquiera para los reyes.

The user soon finds that Homograf is very simple to manage. However, for this application to be really useful it might be advisable to know a little more. Remember that in order to draw architecture properly with a machine one must first have learnt the basic principles of technical drawing and for this, apart from the ability to imagine projections in space, it is essential to know some geometry. Perhaps we should also mention that it takes practice to learn this science. As Euclid said to Ptolemy I, Pharaoh of Egypt, in 300 B.C.: although the king can travel on royal roads, there is no royal road which leads to geometry.